در دنیای ریاضی مسائلی وجود دارند که ساده به نظر میرسند؛ آنقدر ساده که هرکسی با دانشی ابتدایی از ریاضی میتواند آنها را درک کند؛ اما اثبات این مسائل بهقدری دشوار است که هیچکس موفق به حل آنها نشده است. در ادامه با فهرستی از مسائل بهظاهر ساده ریاضی که البته حلشان مشکل است، آشنا خواهید شد.
حدس اعداد اول دوقلو
اعداد اول، اعدادی هستند که تنها بر خودشان و یک بخشپذیرند. تا آنجاییکه ما میدانیم، تعداد اعداد اول بیشمار است و ریاضیدانان سخت درتلاش برای یافتن بزرگترین عدد اول بعدی هستند.
اما تعدادی از اعداد اول هستند که حاصل تفریق آنها ۲ است، مثل ۴۱ و ۴۳. آیا تعداد این اعداد نیز بینهایت است؟ هرچه اعداد اول بزرگتر میشوند، یافتن این دوقلوها (twin primes) سختتر میشود؛ اما از لحاظ تئوری این اعداد نیز باید بینهایت باشند. مشکل اینجا است که هنوز هیچکسی نتوانسته این بینهایتبودن اعداد اول دوگانه را اثبات کند.
مسئله حرکتدادن مبل
اکثر ما احتمالاً هنگام اثاثکشی به خانه جدید با مشکل جابهجاکردن مبل و حرکتدادن آن از میان راهروهای تنگ و کنج دیوار روبهرو شدهایم. سوالی که برای ریاضیدانان پیش میآید، این است: بزرگترین مبلی که بدون در نظر گرفتن شکل آن میتوانید بدون خم کردنش، از گوشه دیواری با زاویهی ۹۰ درجه عبور دهید، چه ابعادی دارد؟
البته ریاضیدانان این مبل را تنها در بُعد در در نظر میگیرند و کاری به کاربرد آن در دنیای واقعی ندارند. جالب است بدانید بزرگترین حجمی که بتواند در کنج یک زاویه ۹۰ درجه جا شود، «ثابت مبل» (Sofa Constant) نامیده میشود. هیچکس بهطور دقیق نمیداند این عدد چقدر است؛ اما مبلهایی هستند که در این زاویه جا میشوند و مبلهایی هستند که جا نمیشوند. برای همین میدانیم که این ثابت باید چیزی بین ابعاد این دو حالت باشد. درحالحاضر تنها چیزی که دربارهی این مسئله میدانیم این است که ثابت مبل باید چیزی بین ۲٫۲۱۹۵ و ۲٫۸۲۸۴ باشد.
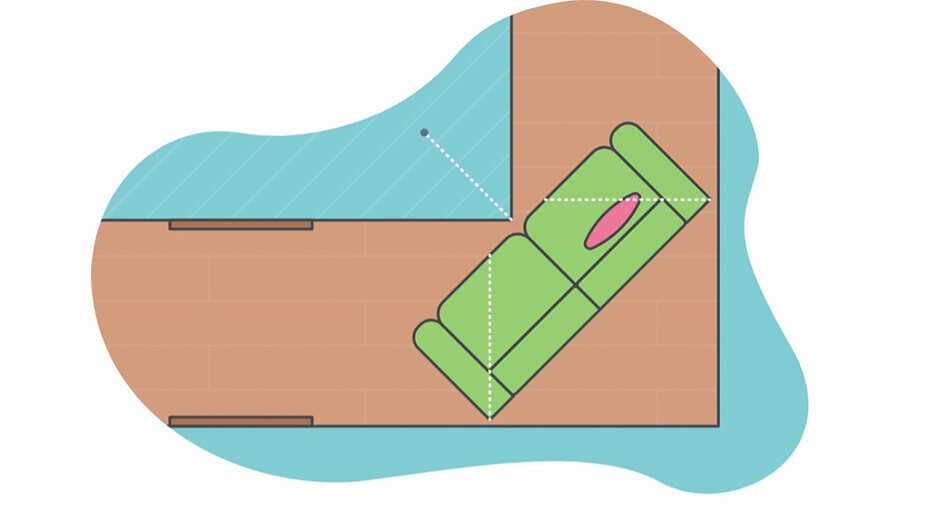
ولی ما مبلهای بزرگی داریم که میدانیم این عدد حداقل بهبزرگی آنها است. ما همچنین مبلهایی داریم که اندازهی آنها با این مقدار سازگار نیست، پس این اندازه از آنها کوچکتر است. درمجموع میدانیم که ثابت مبل چیزی بین ۲.۲۱۹۵ تا ۲.۸۲۸۴ است.
حدس کولاتز
حدس کولاتز (Collatz conjecture) یکی از مشهورترین مسائل حلنشدهی ریاضی است و ازآنجاکه بسیار ساده به نظر میرسد، میتوانید آن را برای کودکان دبستانی توضیح دهید و آنها احتمالاً آنقدر از این مسئله خوششان بیاید که بخواهند جوابی برایش پیدا کنند.
مسئله کولاتز به این صورت است:
ابتدا یک عدد بهدلخواه انتخاب کنید. اگر این عدد زوج بود، آن را به ۲ تقسیم کنید و اگر فرد بود آن را در ۳ ضرب و سپس با ۱ جمع کنید. این مراحل را برای عدد جدید بهدستآمده ادامه دهید. عددی که سرانجام به آن میرسید، همیشه ۱ خواهد بود. بهعنوان مثال اگر عدد انتخابی ۶ باشد، انجام این مراحل، این اعداد را نشان خواهد داد: ۶، ۳، ۱۰، ۵، ۱۶، ۸، ۴، ۲، ۱.
ریاضیدانان میلیونها عدد پیدا کردهاند که از این قاعده پیروی میکند؛ اما مشکل اینجا است که هنوز نتوانستهاند عددی پیدا کنند که طبق این قاعده پیش نرود. احتمال دارد که عددی بسیار بزرگ که میل به بینهایت دارد یا عددی که در یک چرخه گیر کند، هرگز به یک نرسد؛ ولی تابهحال کسی نتوانسته این عدد را پیدا کند.
حدس گلدباخ
حدس گلدباخ (Goldbach’s conjecture) نیز مانند حدس اعداد اول دوقلو، مسئله حلنشده دیگری دربارهی اعداد اول است که بهظاهر ساده اما حل آن بهشدت دشوار است. این مسئله میگوید آیا هر عدد صحیح زوج بزرگتر از ۲، مجموع دو عدد اول است؟ شاید بگویید واضح است که پاسخ مثبت است؛ چراکه عدد ۴ مجموع دو عدد اول ۳ و ۱ یا عدد ۶ مجموع دو عدد اول ۵ و ۱ است و این روند بههمینصورت ادامه دارد.
راستش را بخواهید، این مسئله از نظر کریستین گلدباخ، ریاضیدان آلمانی، که آن را در سال ۱۷۴۲ مطرح کرد، به همین شکل حل شده بود. او با اطمینان کامل گفته بود «هر عدد صحیح زوج بزرگتر از ۴ میتواند بهصورت مجموع دو عدد اول نوشته شود.»
اما با وجود قرنها تلاش، تابهحال هیچکس نتوانسته است ثابت کند که این قاعده همیشه و برای تمام اعداد جواب میدهد. حقیقت این است که اگر ما اعداد را بزرگ و بزرگتر کنیم و بههمین روند ادامه دهیم، شاید به عددی برسیم که برابربا مجموع دو عدد اول نباشد یا به عددی برسیم که تمامی قوانین و منطقی را که تابهحال از آن استفاده میکردیم، نقض کند. بیشک ریاضیدانان تا جوابی برای این مسئله پیدا نکنند، دست از تلاش برنخواهند داشت.
تا به امروز، حدس گلدباخ برای همه اعداد صحیح زوج تا ۴ در ۱۰۱۸ تأیید شده است؛ اما اثبات تحلیلی آن هنوز از دسترس ریاضیدانان دور است. بااینحال، اجماع عمومی بر این است که این حدس بهخاطر ماهیت توزیع اعداد اول درست است. چراکه هرچه یک عدد صحیح بزرگتر باشد، احتمال بیشتری وجود دارد که بتوان آن را به صورت مجموع دو عدد دیگر بیان کرد. بنابراین، هرچه یک عدد صحیح بزرگتر باشد، احتمال اینکه حداقل یکی از این ترکیبها فقط از اعداد اول تشکیل شده باشد، بیشتر است.
۵۸۵۸


